Hauptinhalt

H. A. Schmitt: Vorlesung über Differential- und Integralrechnung

Schmidts Auffassung von Mathematik, seine höchst ausgefeilte, individuelle Zeichensprache und formale Beweismethode lassen sich besonders schön an der Vorlesungsmitschrift seiner Grundvorlesung über Analysis, „Differential- und Integralrechnung I und II“ vom WS 1966/67 und SS 1967 ablesen.
Der  Ausschnitt von Seite 12 der Mitschrift enthält

4.3. Satz: Für alle reellen a ist |a|>= 0 .

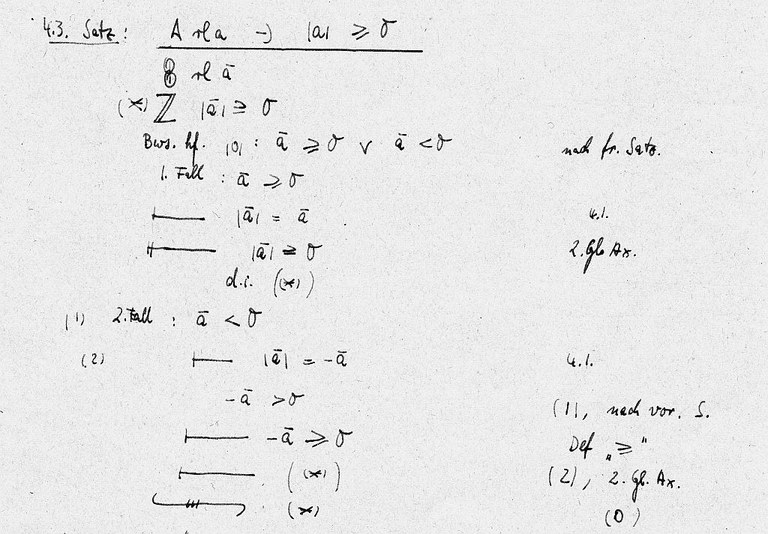
Er wird ausführlich bewiesen, nach einigen Vorbereitungen werden die Fälle a>= 0 , a < 0 behandelt, wobei die Symbole für  „folgt aus der letzten Zeile“ und „folgt aus den letzten beiden Zeilen“ verwendet werden , z.B.
1. Fall: a>= 0
|a| = a
|a| >= 0.

Dies ist keineswegs der einzige Satz über den Betrag, so finden sich unter anderem die Sätze:
Der Betrag ist für alle a definiert, |a| = –a falls a <= 0 und aus a ungleich 0 folgt |a| > 0, alles mit ähnlich ausführlichen Beweisen durch Fallunterscheidung.


Auf Seite 61 der Mitschrift steht mit 12.2 Satz (Ein Höchsteinzigkeitssatz) ein Resultat, was sich wohl in keinem Lehrbuch und keiner anderen Vorlesung zur Analysis wiederfindet.

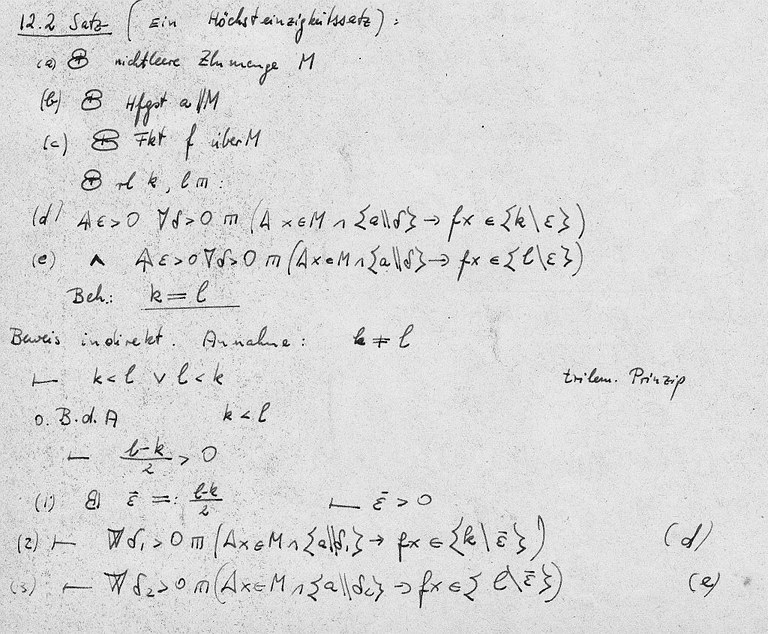
Der Inhalt erschließt sich auch erst nach genauerer Lektüre:

Ist f eine Funktion auf einer Menge M reeller Zahlen, a eine Häufungsstelle von M , k und l reelle Zahlen, so dass gilt:
für alle  > 0 existiert ein  > 0 mit der Eigenschaft: ist x in der punktierten -Umgebung von a, so ist f(x) in der -Umgebung von k     und
für alle > 0 existiert ein  > 0 mit der Eigenschaft: ist x in der punktierten -Umgebung von a, so ist f(x) in der -Umgebung von l .
Dann ist k=l .

Der Beweis erstreckt sich noch über die nächste Seite, immerhin wird hier die Fallunterscheidung k<l , l<k durch o.B.d.A. k<l abgekürzt.

In einer „modernen“ Formulierung  (z.B. Mangoldt-Knopp: Einführung in die höhere Mathematik, Leipzig, 1944) lautet der Höchsteinzigkeitssatz:
„Der Grenzwert einer Zahlenfolge (und Funktion) ist eindeutig.“

Ob die Schmidt‘sche Darstellung zu einer größeren Klarheit und Präzision beitrug, ist umstritten, sicher ist, dass sie mit einem erheblichen Zeitaufwand verbunden war: In der Mitschrift nimmt der Beweis des Zwischenwertsatzes mit allen Hilfssätzen über 10 Seiten ein, der Satz erscheint auch erst im ersten Drittel des zweiten Teils der Vorlesung. Der Teil II endet mit dem „ersten Teil des Fundamentalsatzes der Diff-Int-Rechnung“. Bemerkenswert ist auch, was dazwischen nicht vorkommt: Unendliche Reihen, Beispiele von Funktionen außer der mit Jota bezeichneten Identität j(x)=x und 1/j(x)=1/x, also insbesondere keine Polynome, Wurzelfunktionen, Exponentialfunktion, Logarithmus, trigonometrische Funktionen, ...
Im ersten Teil gibt es ein (einziges) Beispiel, die bereits erwähnte Funktion 1/x, Skizzen fehlen vollständig.
Auch der Ablauf der Vorlesung folgte festen Regeln: so war z.B. die erste Bankreihe mit den Assistenten und Hilfskräften besetzt, die neben dem Tafeldienst auf Zuruf die passenden Formelnummern heraussuchen mussten. In den Prüfungen wurden die Sätze übrigens nach den Nummern abgefragt.