Hauptinhalt
Workshop-Angebote für Schulen
Der Fachbereich bietet Workshops für Schülerinnen und Schüler zu verschiedenen Themen der Mathematik. Bei Interesse kontaktieren Sie bitte die Anbieterin oder den Anbieter.
Aktuell werden Workshops zu folgenden Themen angeboten.
„Mathe macht KI": Osterferiencamp (14.4.-17.4. 2025)
(Eine Kooperation mit dem Schüler:innen-Forschungszentrum Mittelhessen)

Du findest KI interessant und magst Mathe? In einem viertägigen Kurs der Philipps-Universität Marburg erleben Schülerinnen und Schüler ab der 10. Klasse Anwendungen künstlicher Intelligenz. Wir beschäftigen uns mit KI in der Bildklassifizierung sowie in Filmeratings. Wie erkennt eine KI, welche Farbe eine Ampel hat? Warum werden dir bestimmte Filme auf Netflix vorgeschlagen? Was ist dabei der mathematische Hintergrund? Von Punkten und Geraden in der Ebene, über Vektoren bis zu Matrizen gehen wir gemeinsam der Mathematik dahinter auf den Grund. Vorkenntnisse sind in keinem der Themen nötig. Wir werden alles vor Ort lernen, was gebraucht wird.
Voraussichtlicher Ablauf: Di - Fr 9:30 - 15 Uhr (incl. Mittagspause), am Mittwoch Spielenachmittag; optionales Ergänzungsangebot: Schnupperstudium
- Teilnehmende: Klassenstufen 10-13.
- Thematische Anbindung: Mathematik / Informatik / KI.
- Länge: 4 Tage, ca 5 Stunden pro Tag
- Ort: Lahnberge, Mehrzweckgebäude, Hans-Meerwein-Straße 6
- Anmeldung: über SFZ Mittelhessen
„Krumme Sachen“: Welche mathematischen Konsequenzen es hat, dass die Erde keine Scheibe ist (Prof. Ilka Agricola)

In der Schule beschäftigt man sich vor allem mit der ebenen Geometrie von Geraden, Kreisen und Dreiecken – doch auf das Leben auf der runden Erde sind diese Ergebnisse nicht anwendbar. Was bedeutet dies etwa für das Zeichnen von Landkarten und die Navigation?
- Teilnehmer: Klassenstufen 9-13. Maximal 25 Teilnehmer.
- Thematische Anbindung: Mathematik / Erdkunde.
- Länge: ca. 2-2 ½ Stunden (Arbeitsphasen sind darin integriert).
- Ort: In der Schule oder auf den Lahnbergen.
Mathematik des Wählens (Prof. Ilka Agricola)
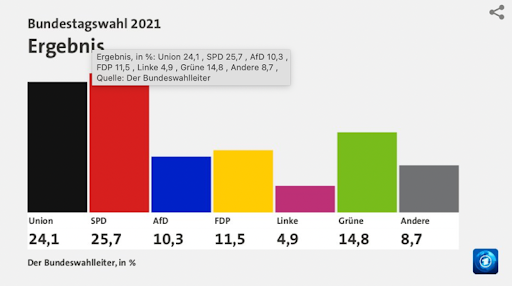
Wenn die Zweitstimmen für die Bundestagswahl ausgezählt sind, ist alles klar – oder doch nicht? Die Stimmenanteile der Parteien sind immer „krumme“ Zahlen, die Anzahl der Abgeordneten einer Fraktion dagegen muss eine ganze Zahl sein. Diese zu bestimmen ist eine mathematisch komplexe Frage – weil dieses sog. „Zuteilungsverfahren“ gewisse Mindestansprüche erfüllen sollte (etwa die „Monotonie“: Wenn eine Partei mehr Stimmen bekommt, darf die Anzahl Fraktionssitze nicht sinken). Der Workshop widmet sich genau diesen Fragen und ihrer direkten Bedeutung für eine parlamentarische Demokratie.
- Teilnehmer: Die Inhalte können variabel für eine Gruppe von SuS der Klassenstufen 5-13 angeboten werden. Maximal 25 Teilnehmer.
- Keine benötigten Vorkenntnisse.
- Thematische Anbindung: Mathematik / Politik und Wirtschaft.
- Länge: ca. 2-2 ½ Stunden (Arbeitsphasen sind darin integriert).
- Ort: In der Schule oder auf den Lahnbergen.
Mathematische Modellsammlung (Prof. Ilka Agricola)

Wie hat man vor dem digitalen Zeitalter komplizierte Rechnungen durchgeführt oder Landkarten vervielfältigt? Die reiche Mathematische Modellsammlung des Fachbereichs Mathematik und Informatik der Philipps-Universität gibt hierzu spielerisch und kurzweilig Auskunft – und noch zu vielem mehr.
- Teilnehmer: Die Inhalte können variabel für eine Gruppe von SuS der Klassenstufen 9-13 angeboten werden. Maximal 20 Teilnehmer.
- Thematische Anbindung: Mathematik / Physik.
- Länge: ca. 2-2 ½ Stunden (Arbeitsphasen sind darin integriert).
- Ort: Auf den Lahnbergen.
- Weitere Informationen: https://www.uni-marburg.de/de/fb12/fachbereich/profil/modellsammlung
Mit Schülern Einstein’s Leben und Werk entdecken (Prof. Ilka Agricola)

Einstein kennt jeder – aber meist sind dies eher Cliches. Der Workshop ist zweigeteilt.
Teil 1 (immer gleich): Was ist dran an den Cliches – war Einstein wirklich schlecht in Mathe und ein Rebell, was sind die Grundaussagen der Relativitätstheorie, und muss man ein Genie sein, um dies zu verstehen?
Teil 2 (je nach Vorkenntnissen und Zusammensetzung der Gruppe):
Variante A: Grundlagen der speziellen Relativitätstheorie gemeinsam erarbeiten (thematische Anbindung: Mathematik, Physik - Einsteigerniveau)
Variante B: Einsteins Brief an Roosevelt vom 11.10.1939 gemeinsam lesen, verstehen, deuten (thematische Anbindung: Geschichte, Englisch)
Variante C: Herleitung der Formel E=mc² aus grundlegenden Prinzipien der Physik (thematische Anbindung: Mathematik, Physik – fortgeschrittenes Niveau)
- Teilnehmer: Klassenstufen 10-13. Maximal 25 Teilnehmer.
- Thematische Anbindung: Je nach Wahl des 2. Teils an Mathematik / Physik oder Geschichte / Englisch.
- Länge: ca. 2-2 ½ Stunden (Arbeitsphasen sind darin integriert).
- Ort: In der Schule oder auf den Lahnbergen.
Geometrie und Topologie: über Landkarten, Donuts und Kartoffelchips (Prof. Oliver Goertsches)

In diesem Workshop beschäftigen wir uns mit einigen Objekten und Fragestellungen aus der nach Bernhard Riemann benannten Riemannschen Geometrie, in der man Abstände, Winkel, Flächeninhalt und Volumen in gekrümmten Räumen betrachtet. Unter anderem werden wir versuchen, die optimale Weltkarte zu erstellen, die Krümmung von Donuts, Pizza und Kartoffelchips untersuchen, den Unterschied zwischen Topologie und Geometrie kennenlernen, und die Angst vor vielen Dimensionen verlieren.
- Ort: Lahnberge
- Länge: 2-3 Stunden
Flächenbestimmung von Polygonen (Prof. Istvan Heckenberger)
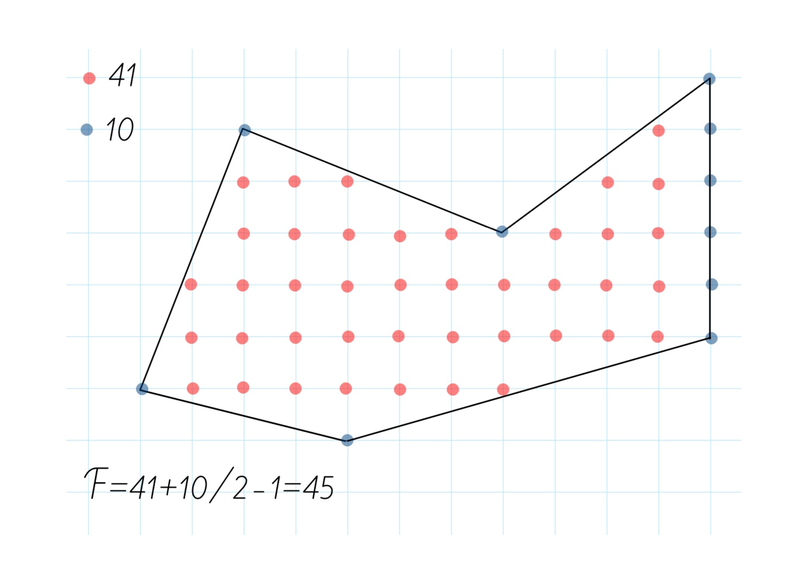
Die Bestimmung der Fläche von Dreiecken und bestimmten Vierecken ist bekanntermassen recht einfach. Vielecke dagegen können sehr ungewöhnliche Formen annehmen und man vermutet komplexere Formeln. Umso überraschender ist es, dass es sogar mehrere sehr einfache Berechnungsverfahren gibt. Beim Workshop lernt man verschiedene Ideen zur Flächenbestimmung kennen, macht sich mit den Berechnungsmethoden und mit den zugehörigen Hintergründen vertraut und man hat die Möglichkeit, die Methoden an vielen Beispielen miteinander zu vergleichen.
- Ort: Lahnberge
- Länge: etwa 2 Stunden
Von Schlüsseln und Falltüren - ein Streifzug durch die Kryptographie (Prof. Patrick
Mehlitz)

Die Verschlüsselung von Daten vor ihrem Transport über (unsichere) Transportwege ist gerade jetzt, im digitalen Zeitalter, von essentieller Bedeutung - beispielsweise im Kontext bargeldloser Bezahlung. Der Workshop vermittelt einen Überblick über verschiedene klassische und moderne Verschlüsselungstechniken. Wir erarbeiten uns anschaulich den essentiellen Unterschied zwischen sogenannten öffentlichen und privaten Schlüsseln. Ferner befassen wir uns mit den mathematischen Grundlagen der Kryptographie - dem Rechnen in sogenannten Restklassenringen. Natürlich werden wir einige einfache Algorithmen gemeinsam anhand kleiner Kryptogramme ausprobieren und den zu ihrer Erzeugung verwendeten DPEF knacken.
- Teilnehmer: Klassenstufe 5-12 (Themenschwerpunkte orientieren sich an der Altersstruktur)
- Länge: 2-3 Stunden
- Ort: in der Schule oder auf den Lahnbergen
Wenn sich Mathematiker entscheiden müssen... (Prof. Patrick Mehlitz)
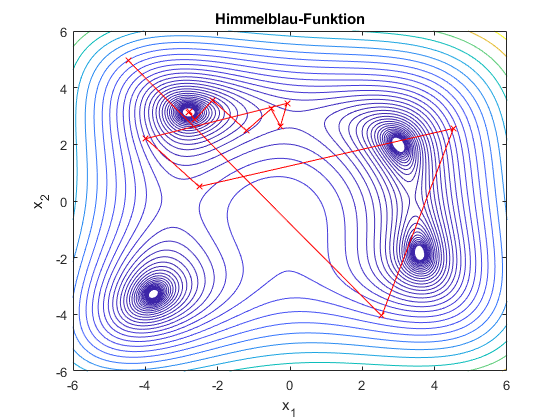
Der Workshop vermittelt einen Einblick in das Gebiet der mathematischen Optimierung, die sich damit befasst, aus einer vorgegebenen Menge von Entscheidungsalternativen die bzgl. eines Qualitätsmaßes bestmögliche Option auszuwählen. Typische Anwendungen der mathematischen Optimierung sind beispielsweise
- die Bestimmung kürzester Wege zwischen einem Start- und Zielort (Routenplanung),
- bestmögliche Versorgung von Supermärkten mit Lebensmitteln aus Lagern (Transportproblem),
- Zusammenstellung eines risikominimalen Aktienportfolios mit Mindestrendite (Portfoliooptimierung),
- Trainieren neuronaler Netzwerke (maschinelles Lernen).
Wir befassen uns zunächst mit einigen Grundbegriffen der mathematischen Optimierung. Danach erschließen wir uns, wie man gewisse lineare Optimierungsaufgaben einfach graphisch lösen kann. Anschließend beleuchten wir einige Beispielklassen von Optimierungsproblemen näher. Zuletzt untersuchen wir, inwieweit die Differentialrechnung zur Lösung nichtlinearer Optimierungsaufgaben genutzt werden kann (je nach Kenntnisstand der Teilnehmenden).
- Teilnehmer: Klassenstufe 9-12 (Themenschwerpunkte orientieren sich an der
Altersstruktur) - Länge: 2-3 Stunden
- Ort: in der Schule oder auf den Lahnbergen