Main Content
Bayesian statistics and hierarchical modeling
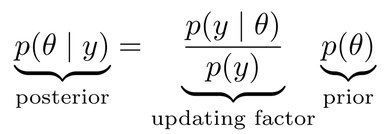
In psychological research, Bayesian statistics is increasingly used to draw statistical conclusions. In contrast to classical, frequentist statistics, Bayesian statistics allows researchers a more intuitive interpretation of parameter estimates and uncertainty intervals (e.g., "the difference between two means is in the interval [0.24, 0.36] with 95% probability") and hypothesis testing (e.g., "for the observed data, the null hypothesis is 10 times more likely than the alternative hypothesis"). To make such statements about the "posterior distribution" (i.e., about the distribution of the most likely values of parameter given the observed data), it is necessary to define a statistical model (the "likelihood function") as well as to make prior assumptions about plausible values of the parameters (the "prior" distribution).
In our research, we use Bayesian statistics for statistical and cognitive modeling and testing of psychological theories, particularly in the context of hierarchical models which assume separate parameters for different individuals. In addition, we are interested in the implementation of these methods in the statistical software R as well as possible errors that can happen during their application. Furthermore, it is of interest to contrast Bayesian statistics and frequentist methods in order to give recommendations for their application in practice.
Relevant publications:
- Heck, D. W., & Bockting, F. (in press). Benefits of Bayesian model averaging for mixed-effects modeling. Computational Brain & Behavior. https://doi.org/10.1007/s42113-021-00118-x
- Heck, D. W., et al. (in press). A review of applications of the Bayes factor in psychological research. Psychological Methods. https://psyarxiv.com/cu43g
- Heck, D. W. (2019). A caveat on the Savage-Dickey density ratio: The case of computing Bayes factors for regression parameters. British Journal of Mathematical and Statistical Psychology, 72, 316-333. https://doi.org/10.1111/bmsp.12150
- Heck, D. W. (2019). Accounting for estimation uncertainty and shrinkage in Bayesian within-subject intervals: A comment on Nathoo, Kilshaw, and Masson (2018). Journal of Mathematical Psychology, 88, 27-31. https://doi.org/10.1016/j.jmp.2018.11.002
- Heck, D. W., & Bockting, F. (in press). Benefits of Bayesian model averaging for mixed-effects modeling. Computational Brain & Behavior. https://psyarxiv.com/zusd2/
- Heck, D. W., Boehm, U., ... & Hoijtink, H. (in press). A review of applications of the Bayes factor in psychological research. Psychological Methods. PsyArXiv. https://psyarxiv.com/cu43g
- Heck, D. W., & Davis-Stober, C. P. (2019). Multinomial models with linear inequality constraints: Overview and improvements of computational methods for Bayesian inference. Journal of Mathematical Psychology, 91, 70-87. https://doi.org/10.1016/j.jmp.2019.03.004
- Heck, D. W., Wagenmakers, E., & Morey, R. D. (2015). Testing order constraints: Qualitative differences between Bayes factors and normalized maximum likelihood. Statistics & Probability Letters, 105, 157-162. https://doi.org/10.1016/j.spl.2015.06.014
- Heck, D. W., & Wagenmakers, E. (2016). Adjusted priors for Bayes factors involving reparameterized order constraints. Journal of Mathematical Psychology, 73, 110-116. https://doi.org/10.1016/j.jmp.2016.05.004
- Gronau, Q. F., Wagenmakers, E., Heck, D. W., & Matzke, D. (2019). A simple method for comparing complex models: Bayesian model comparison for hierarchical multinomial processing tree models using warp-III bridge sampling. Psychometrika, 84, 261–284. https://doi.org/10.1007/s11336-018-9648-3