Main Content

Morphology–Transport Relationships for Packed Columns

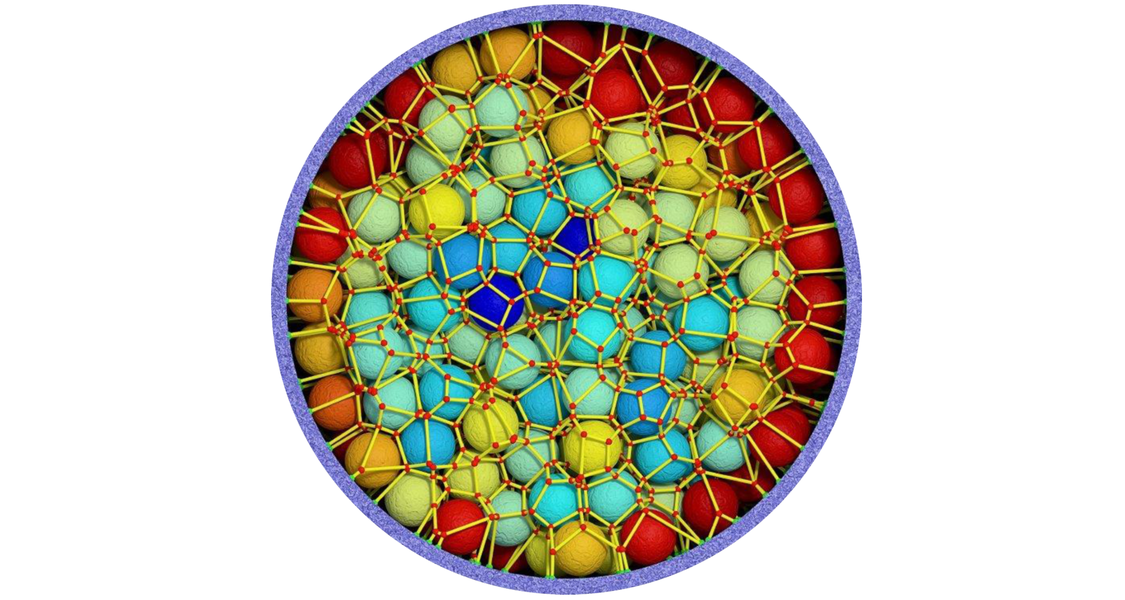
Liquid chromatography is an industrially relevant application of mass transport through a porous medium, where a fluid mix of chemical substances is separated into its components by passing through a cylindrical tube densely packed with solid, spherical adsorbent particles (the column). The number of chemical substances that can be separated by a column (its separation efficiency) is determined by how the packing particles are distributed over the column volume. However, the packing morphology of chromatographic columns, which are packed "as good as possible" following empirically developed protocols, is generally unknown, as is the relation between packing morphology and separation efficiency.

By simulating fluid flow through computer-generated, confined sphere packings we correlate morphological parameters with transport coefficients (S. Khirevich et al., Journal of Chromatography A 2012, 1262, 77–91). A packing is a mechanically stable, disordered distribution of solid spheres inside a cylindrical tube; fluid flows through the void space between the spheres. Our approach allows a systematic and independent variation of decisive morphological parameters, which is impossible with real chromatographic columns: the column diameter, the packing porosity (the void space fraction of the column), and the degree of packing disorder (the void space distribution in the column). We used an advanced geometrical approach to quantify the degree of disorder across the column diameter. The figure shows a packing cross-section, where each sphere is surrounded by a polygonal cell that encloses all space points closer to this sphere than to any of its neighbors. Spheres are colored to indicate the volume of their surrounding cell (from red for large to blue for small volumes). Cell volumes increase from the denser core to the looser edge of the packing. The extent to which cell volumes at the edge deviate from those in the core of the packing (calculated over radial profiles for the whole packing length) determines the transcolumn disorder. The higher the transcolumn disorder, the lower the separation efficiency.

The simulation of fluid flow in a sphere packing is a highly demanding computational task, because (i) the solid–void borders (around each sphere and at the cylindrical wall) need to be finely resolved to receive accurate transport data, and (ii) the length scales on which mass transport occurs require sufficiently long packings (~10³ sphere diameters), resulting in very large systems (~10⁶ spheres).

Acknowledgement. Computational resources on IBM BlueGene/Q systems were provided by Forschungszentrum Jülich (FZJ, Jülich, Germany). We thank the John von Neumann Institute for Computing (NIC) and the Jülich Supercomputing Center (JSC) at FZJ for the allocation of several CPU-time grants over the past years (NIC Project Nos. 4717, 8214, and 10214, JSC Project ID: HMR10).